1.
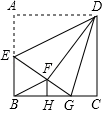
如图,点  是正方形
是正方形  边
边  上一点,连接
上一点,连接  ,作
,作  于点
于点  ,
,  手点
手点  ,连接
,连接  .
.
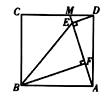
(1)
求证:  ;
(2)
已知
;
(2)
已知  ,四边形
,四边形  的面积为24,求
的面积为24,求  的正弦值.
的正弦值.
【考点】
全等三角形的判定与性质;
正方形的性质;
锐角三角函数的定义;