已知：如图，在半径为4的⊙O中，AB、CD是两条直径，M为OB的中点，CM的延长线交⊙O于点E，且EM＞MC．连接DE，DE= ．

0 返回出卷网首页

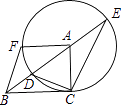
1. 已知：如图，在半径为4的⊙O中，AB、CD是两条直径，M为OB的中点，CM的延长线交⊙O于点E，且EM＞MC．连接DE，DE= $\text{[math]}$ ．

(1) 求证：AM•MB=EM•MC；

(2) 求EM的长；

(3) 求sin∠EOB的值．

【考点】

圆周角定理; 相似三角形的判定与性质; 锐角三角函数的定义;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，在Rt△ACB中，∠ACB=90°，以点A为圆心，AC长为半径的圆交AB于点D，BA的延长线交⊙A于点E，连接CE，CD，F是⊙A上一点，点F与点C位于BE两侧，且∠FAB=∠ABC，连接BF．

(1) 求证：∠BCD=∠BEC；

(2) 若BC=2，BD=1，求CE的长及sin∠ABF的值．

综合题普通

2. 如图1：以x轴的正半轴上一点O₁为圆心作⊙O₁ ，交x轴于C、D两点，交y轴于A、B两点，以O为圆心OA为半径的⊙O与x轴的负半轴交于G点.设⊙O₁的弦AC的延长线交⊙O于F点，连结GF，AG，若AO＝4， $\text{[math]}$

(1) 求证：△AGC∽△AFG；

(2) 求出点O₁的坐标；

(3) 如图2，线段EA、EB（或它们的延长线）分别交⊙O于点M、N.问：当点E在 $\text{[math]}$ （不含端点A、B）上运动时，线段MN的长度是否会发生变化？若不变，求出MN的长度；若变化，请说明理由.

综合题困难

3. 如图，已知在 $\text{[math]}$ 中， $\text{[math]}$ ，点O在边 $\text{[math]}$ 上，以 $\text{[math]}$ 为半径的 $\text{[math]}$ 与 $\text{[math]}$ 边切于点D， $\text{[math]}$ 与 $\text{[math]}$ ， $\text{[math]}$ 边的另一交点分别为E，F.

(1) 求证： $\text{[math]}$ .

(2) 若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的半径.

综合题普通