1.
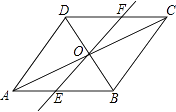
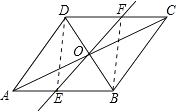
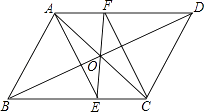
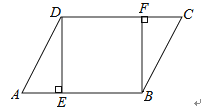
如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=CD,连接CF.

(1)
求证:△AEF≌△DEB;
(2)
若AB=AC,试判断四边形ADCF的形状,并证明你的结论.
【考点】
全等三角形的判定与性质;
平行四边形的性质;
矩形的判定;