0 返回出卷网首页
1. 在△ABC中，AB＝AC，P是BC上任意一点．

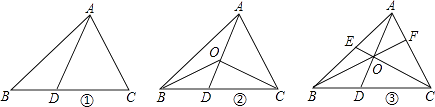
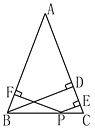
(1) 如图①，若P是BC边上任意一点，PF⊥AB于点F，PE⊥AC于点E，BD为△ABC的高线，试探求PE，PF与BD之间的数量关系；
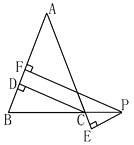
(2) 如图②，若P是BC延长线上一点，PF⊥AB于点F，PE⊥AC于点E，CD为△ABC的高线，试探求PE，PF与CD之间的数量关系．
【考点】
三角形的面积; 等腰三角形的性质;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1. 如图，在正方形网格中，每一小正方形的边长为1，格点ABC（三个顶点在相应的正方形的顶点处）在如图所示的位置：

(1) △ABC的面积为：；
(2) 在网格中画出线段AB绕格点P顺时针旋转90°之后的对应线段A1B1；
(3) 在（2）的基础上，直接写出 =．
综合题 普通
2. 如图，在平面直角坐标系中一次函数 的图象分别交x、y轴于点A、B，与一次函数y=x的图象交于第一象限内的点C．

(1) 分别求出A、B、C、的坐标；
(2) 求出△AOC的面积．
综合题 普通
3. 如图，在△ABC中，D是BC边上的点（不与点B、C重合），连结AD．

问题引入：

(1) 如图①，当点D是BC边上的中点时，S△ABD：S△ABC=；当点D是BC边上任意一点时，S△ABD：S△ABC=（用图中已有线段表示）．

探索研究：
(2) 如图②，在△ABC中，O点是线段AD上一点（不与点A、D重合），连结BO、CO，试猜想S△BOC与S△ABC之比应该等于图中哪两条线段之比，并说明理由．

拓展应用：
(3) 如图③，O是线段AD上一点（不与点A、D重合），连结BO并延长交AC于点F，连结CO并延长交AB于点E，试猜想 + + 的值，并说明理由．
综合题 普通