1.
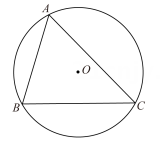
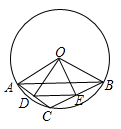
如图是一块残缺的圆轮片,点A、C在圆弧上.

(1)
用尺规作出  的中点B,再作出△ABC的外接圆(不写作法,保留作图痕迹).
(2)
若
的中点B,再作出△ABC的外接圆(不写作法,保留作图痕迹).
(2)
若  ,
,  ,求外接圆的半径.
,求外接圆的半径.
【考点】
垂径定理;
三角形的外接圆与外心;