如图，正方形网格中每个小正方形边长都是1.

0 返回出卷网首页

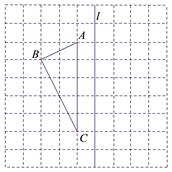
1. 如图，正方形网格中每个小正方形边长都是1.

(1) 画出△ABC关于直线l对称的图形△A₁B₁C₁；

(2) 在直线l上找一点P，使PB＝PC；（要求在直线l上标出点P的位置）

(3) 连接PA、PC，计算四边形PABC的面积．

【考点】

三角形的面积; 轴对称的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

作图题普通

1. 如图，在边长为1的正方形组成的网格中， $\text{[math]}$ 的顶点均在格点上，A（-3，2），B（-4，-3），C（﹣1，﹣1）．

(1) 画出 $\text{[math]}$ 关于y轴对称的图形 $\text{[math]}$ ；

(2) 写出 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 的坐标（直接写出答案） $\text{[math]}$ ； $\text{[math]}$ ； $\text{[math]}$ ；

(3) 写出 $\text{[math]}$ 的面积为．（直接写出答案）

(4) 在y轴上求作一点 P，使得点P到点A与点C的距离之和最小．

作图题普通

2. 方格纸中每个小方格都的边长为1的正方形，我们把以格点连线为边的多边形称为“格点多边形”．

(1) 在图1中确定格点D，并画出一个以A、B、C、D为顶点的四边形，使其为轴对称图形；

(2) 在图2中画一个格点正方形，使其面积等于10；

(3) 直接写出图3中△FGH的面积是．

作图题普通

3. 图①、图②、图③均是4×4的正方形网格，每个小正方形的边长均为1，每个小正方形的顶点叫做格点，△ABC的顶点均在格点上，在图①、图②、图③中分别画一个与△ABC有一条公共边且与ABC成轴对称的三角形，要求所画三角形不完全重合．

作图题普通