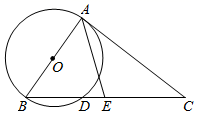
如图，在⊙O中，点A，B，C，D为圆周的四等分点，AE为切线，连接ED．并延长交⊙O于点F，连接BF交AC于点G．

0 返回出卷网首页

1. 如图，在⊙O中，点A，B，C，D为圆周的四等分点，AE为切线，连接ED．并延长交⊙O于点F，连接BF交AC于点G．

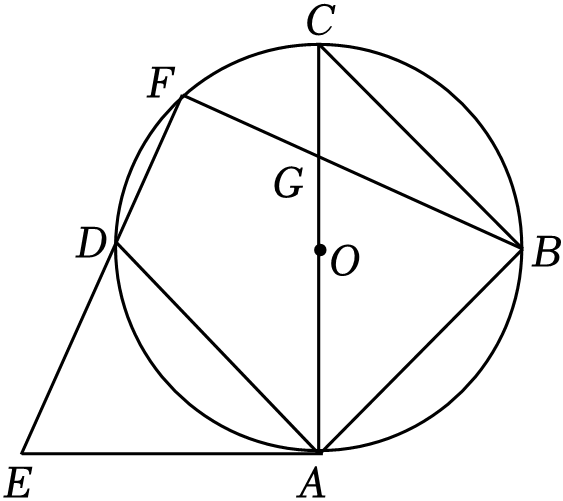
(1) 求证：AD平分∠CAE；

(2) 求证：△ADE≌△ABG；

(3) 若AE＝3，AG＝3GC，求cos∠CBF的值．

【考点】

圆周角定理; 切线的性质; 圆的综合题; 锐角三角函数的定义; 三角形全等的判定-ASA;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，在Rt $\text{[math]}$ 中， $\text{[math]}$ ，以斜边 $\text{[math]}$ 上的中线 $\text{[math]}$ 为直径作⊙O ，与 $\text{[math]}$ 交于点M，与 $\text{[math]}$ 的另一个交点为E，过点M作⊙O的切线 $\text{[math]}$ 交 $\text{[math]}$ 于点N．

(1) 求证： $\text{[math]}$ ；

(2) 若⊙O的直径为5， $\text{[math]}$ ，求 $\text{[math]}$ 的长．

综合题普通

2. 如图，以 $\text{[math]}$ 为直径作 $\text{[math]}$ ，过点A作 $\text{[math]}$ 的切线 $\text{[math]}$ ，连接 $\text{[math]}$ ，交 $\text{[math]}$ 于点D，点E是 $\text{[math]}$ 边的中点，连结 $\text{[math]}$ ．

(1) 求证： $\text{[math]}$ ；

(2) 若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．

综合题普通

3. 如图，AB是⊙O的直径，AC是⊙O的切线，连接OC交⊙O于E ，过点A作AF⊥AC于F交⊙O于D ，连接DE ， BE ， BD

(1) 求证：∠C＝∠BED；

(2) 若AB＝12，tan∠BED＝ $\text{[math]}$ ，求CF的长．

综合题普通