1.
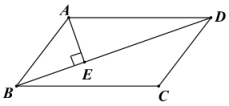
在▱ABCD中,∠C=45°,AD=BD,点P为边CD上的动点(点P不与点D重合),连接AP,过点P作PE⊥AP交直线BD于点E.


(1)
如图①,当点P是边CD的中点时,求证:∠APD=∠EPB;
(2)
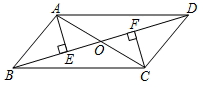
如图②,当点P是边CD上任意点时,
①求证:PA=PE;
②探究线段DE,DA和DP之间的数量关系.
①求证:PA=PE;
②探究线段DE,DA和DP之间的数量关系.
【考点】
三角形全等及其性质;
平行四边形的性质;
三角形全等的判定-AAS;