等腰Rt△PAB中，∠PAB＝90°，点C是AB上一点（与A、B不重合），连接PC，将线段PC绕点C顺时针旋转90°，得到线段DC．连接PD，BD．探究∠PBD的度数，以及线段AB与BD、BC的数量关系．

0 返回出卷网首页

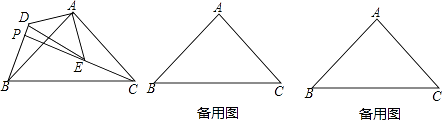
1. 等腰Rt△PAB中，∠PAB＝90°，点C是AB上一点（与A、B不重合），连接PC，将线段PC绕点C顺时针旋转90°，得到线段DC．连接PD，BD．探究∠PBD的度数，以及线段AB与BD、BC的数量关系．

(1) 尝试探究：如图（1），点C在线段AB上，

∵△PCD为等腰直角三角形，且∠PCD＝90°，∴∠CPD＝45°＝∠APB，

∴∠CPD﹣∠BPC＝∠APB﹣∠BPC，即∠BPD＝∠APC，

又∵ $\text{[math]}$ ＝ $\text{[math]}$ ＝ $\text{[math]}$ ，∴△PAC∽△PBD，相似比为 $\text{[math]}$ ＝ $\text{[math]}$ ，∴ $\text{[math]}$ ＝ $\text{[math]}$ ．

∴∠PBD＝；AB＝BC+AC＝．

(2) 类比探索：如图（2），点C在直线AB上，且在点B右侧，还能得出与（1）中同样的结论么？请写出你得到的结论并证明

(3) 拓展迁移：如图（3），点C在直线AB上，且在点A左侧，请补充完成图形，并直接写出你得到的结论（不需要证明）

【考点】

相似三角形的判定与性质; 旋转的性质; 等腰直角三角形;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

(1) 如图， $\text{[math]}$ 和 $\text{[math]}$ 是等腰直角三角形， $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 上，点 $\text{[math]}$ 在线段 $\text{[math]}$ 延长线上，连接 $\text{[math]}$ ， $\text{[math]}$ ．线段 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系为．

(2) 如图2，将图1中的 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ 第一问的结论是否仍然成立；如果成立，证明你的结论，若不成立，说明理由．

(3) 如图3，若 $\text{[math]}$ ，点 $\text{[math]}$ 是线段 $\text{[math]}$ 外一动点， $\text{[math]}$ ，连接 $\text{[math]}$ ，若将 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转90°得到 $\text{[math]}$ ，连接 $\text{[math]}$ ，则 $\text{[math]}$ 的最大值是．

综合题困难

2. 如图，在△ABC中，∠ACB＝90°，AC＝BC ，以C为顶点作等腰直角△CMN ，使∠CMN＝90°，连接BN ，射线NM交BC于点D ．

(1) 如图1，若点A ， M ， N在一条直线上．

①求证：BN+CM＝AM；

②若AM＝6，BN＝2，求BD的长；

(2) 如图2．若AB＝4，CN＝2，将△CMN绕点C逆时针旋转一周，在旋转过程中射线NM交AB于点H ，当三角形DBH是直角三角形时，请你直接写出CD的长．

综合题普通

3. 某学习小组开展了图形旋转的探究活动：将一个矩形 $\text{[math]}$ 绕点A顺时针旋转 $\text{[math]}$ ，得到矩形 $\text{[math]}$ ，连结 $\text{[math]}$ ．

(1) 如图1，当 $\text{[math]}$ 时，点 $\text{[math]}$ 恰好在 $\text{[math]}$ 延长线上．若 $\text{[math]}$ ，求 $\text{[math]}$ 的长．

(2) 如图2，连结 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 于点M．观察思考线段 $\text{[math]}$ 与 $\text{[math]}$ 数量关系并说明理由．

(3) 在（2）的条件下，射线 $\text{[math]}$ 交 $\text{[math]}$ 于点N（如图3），若 $\text{[math]}$ ，旋转角 $\text{[math]}$ 等于多少度时 $\text{[math]}$ 是等边三角形，请写出 $\text{[math]}$ 的值，并说明 $\text{[math]}$ 是等边三角形的理由．

综合题困难