1.
已知AC，EC分别为四边形ABCD和EFCG的对角线，点E在△ABC内，∠CAE+∠CBE=90．
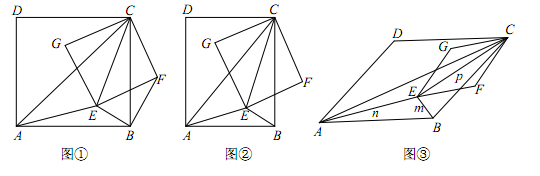
(1)
如图①，当四边形ABCD和EFCG均为正方形时，连接BF．
(2)
如图②，当四边形ABCD和EFCG均为矩形，且 
时，若BE＝1，AE=2，CE=3，求k的值；
(3)
如图③，当四边形ABCD和EFCG均为菱形，且∠DAB=∠GEF=45°时，设BE=m，AE=n，CE=p，试探究m，n，p三者之间满足的等量关系．（直接写出结果，不必写出解答过程）
i）求证：△CAE∽△CBF；
ii）若BE=1，AE=2，求CE的长；
【考点】
菱形的判定与性质;
正方形的性质;
相似三角形的判定与性质;
