1.
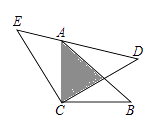
如图,在△ABC中,AB=BC,∠ABC=90°,BM是AC边中线,点D,E分别在边AC和BC上,DB=DE,EF⊥AC于点F,以下结论:
①∠DBM=∠CDE ②.S△BDE<S四边形BMFE ③CD·EN=BE·BD ④AC=2DF.
其中正确结论的个数是( )

A.
1
B.
2
C.
3
D.
4
【考点】
全等三角形的判定与性质;
相似三角形的判定与性质;
等腰直角三角形;
基础巩固
能力提升
变式训练
拓展培优
真题演练