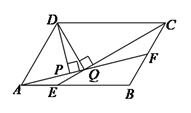1.
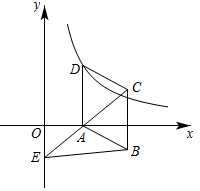
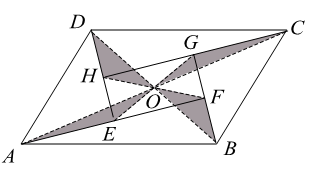
如图,四边形  是平行四边形,点
是平行四边形,点  为
为  的中点,延长
的中点,延长  至点
至点  ,使
,使  ,连接
,连接  、
、  、
、  ,则在
,则在  中
中  ( )
( )

A.
 B.
B.
 C.
C.
 D.
D.

【考点】
三角形的面积;
平行四边形的性质;