1.
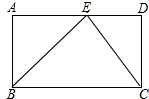
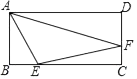
如图，在矩形ABCD中，AD＝4，DC＝3，对角线AC、BD相交于点O，动点P、Q分别从点C、A同时出发，运动速度均为1cm/s，点P沿C→O→B运动．到点B停止，点Q沿A→D→C运动，到点C停止．连接AP、AQ、PQ，设△APQ的面积为y（cm2）（这里规定：线段是面积为0的几何图形），点Q的运动时间为x（s）．
(1)
填空：BO＝cm；
(2)
当PQ∥CD时，求x的值；
(3)
当 
时，求y与x之间的函数关系式；
(4)
直接写出在整运动过程中，使AQ＝PQ的所有x的值．
【考点】
勾股定理;
矩形的性质;
相似三角形的判定与性质;
