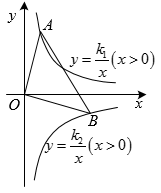
如图，一次函数的图象与反比例函数的图象交于点A与点．

0 返回出卷网首页

1. 如图，一次函数 $\text{[math]}$ 的图象与反比例函数 $\text{[math]}$ 的图象交于点A与点 $\text{[math]}$ ．

(1) 求反比例函数的表达式；

(2) 若动点P是第一象限内双曲线上的点（不与点A重合），连接 $\text{[math]}$ ，且过点P作y轴的平行线交直线 $\text{[math]}$ 于点C ，连接 $\text{[math]}$ ，若 $\text{[math]}$ 的面积为3，求出点P的坐标．

【考点】

坐标与图形性质; 待定系数法求反比例函数解析式;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，A、C分别在坐标轴上，点B的坐标为（4，2），直线 $\text{[math]}$ 交AB，BC分别于点M，N，反比例函数 $\text{[math]}$ 的图象经过点M，N.

(1) 求反比例函数的解析式；

(2) 若点P在y轴上，且△OPM的面积与四边形BMON的面积相等，求点P的坐标.

综合题普通

2. 在平面直角坐标系xOy中，对于任意三点A，B，C的“矩面积”，给出如下定义：“水平底”a：任意两点横坐标差的最大值，“铅垂高”h：任意两点纵坐标差的最大值，则“矩面积”S=ah．例如：三点坐标分别为A（1，2），B（﹣3，1），C（2，﹣2），则“水平底”a=5，“铅垂高”h=4，“矩面积”S=ah=20．根据所给定义解决下列问题：

(1) 若已知点D（1，2）、E（﹣2，1）、F（0，6），则这3点的“矩面积”=．

(2) 若D（1，2）、E（﹣2，1）、F（0，t）三点的“矩面积”为18，求点F的坐标．

综合题普通

3. 已知如图，四边形ABDC坐标为A（9，0），B（5，1），C（5，4），D（2，4）．

(1) 请在边长为1的小正方形组成的网格中建立平面直角坐标系，然后在平面直角坐标系中画出四边形ABDC．

(2) 求四边形ABDC的面积．

综合题普通