如图，抛物线y＝ax2+bx（a＞0）过点E（8，0），矩形ABCD的边AB在线段OE上（点A在点B的左侧），点C、D在抛物线上，∠BAD的平分线AM交BC于点M，点N是CD的中点，已知OA＝2，且OA：AD＝1：3.

0 返回出卷网首页

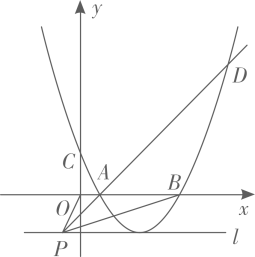
1. 如图，抛物线y＝ax²+bx（a＞0）过点E（8，0），矩形ABCD的边AB在线段OE上（点A在点B的左侧），点C、D在抛物线上，∠BAD的平分线AM交BC于点M，点N是CD的中点，已知OA＝2，且OA：AD＝1：3.

(1) 求抛物线的解析式；

(2) F、G分别为x轴，y轴上的动点，顺次连接M、N、G、F构成四边形MNGF，求四边形MNGF周长的最小值；

(3) 在x轴下方且在抛物线上是否存在点P，使△ODP中OD边上的高为 $\text{[math]}$ ？若存在，求出点P的坐标；若不存在，请说明理由；

(4) 矩形ABCD不动，将抛物线向右平移，当平移后的抛物线与矩形的边有两个交点K、L，且直线KL平分矩形的面积时，求抛物线平移的距离.

【考点】

待定系数法求二次函数解析式; 相似三角形的判定与性质; 二次函数y=ax²+bx+c的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，二次函数的图象经过原点 $\text{[math]}$ 和 $\text{[math]}$ ，与 $\text{[math]}$ 轴交于另一点 $\text{[math]}$ ，且对称轴是 $\text{[math]}$ ．

(1) 求二次函数的表达式；

(2) 若 $\text{[math]}$ 是 $\text{[math]}$ 上的一点，作 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，当 $\text{[math]}$ 的面积最大时，求点 $\text{[math]}$ 的坐标；

(3) $\text{[math]}$ 是 $\text{[math]}$ 轴上的点，过 $\text{[math]}$ 作 $\text{[math]}$ 轴，与抛物线交于点 $\text{[math]}$ ，过 $\text{[math]}$ 作 $\text{[math]}$ 轴于 $\text{[math]}$ ，是否存在点 $\text{[math]}$ ，使以点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 为顶点的三角形与以点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 为顶点的三角形相似？若存在，求出点 $\text{[math]}$ 的坐标；若不存在，请说明理由．

综合题困难

2. 如图，已知抛物线经过原点O，顶点为A(1，1)，且与直线 $\text{[math]}$ 交于B，C两点．

(1) 求抛物线的解析式及点C的坐标；

(2) 求△ABC的面积；

(3) 若点N为x轴上的一个动点，过点N作MN⊥x轴与抛物线交于点M，则是否存在以O，M，N为顶点的三角形与△ABC相似？若存在，请求出点N的坐标；若不存在，请说明理由．

综合题困难

3. 二次函数 $\text{[math]}$ （ $\text{[math]}$ ）的图像经过点A（2，4）、B（5，0）和O（0，0）．

(1) 求二次函数的解析式；

(2) 联结AO，过点B作BC⊥AO于点C，与该二次函数图象的对称轴交于点P，联结AP，求∠BAP的余切值；

(3) 在（2）的条件下，点M在经过点A且与x轴垂直的直线上，当 $\text{[math]}$ AMO与 $\text{[math]}$ ABP相似时，求点M的坐标．

综合题困难