1.
如图所示,二次函数  的图像(记为抛物线
的图像(记为抛物线  )与y轴交于点C,与x轴分别交于点A、B,点A、B的横坐标分别记为
)与y轴交于点C,与x轴分别交于点A、B,点A、B的横坐标分别记为  ,
,  ,且
,且  .
.
(1)
若  ,
,  ,且过点
,且过点  ,求该二次函数的表达式;
(2)
若关于x的一元二次方程
,求该二次函数的表达式;
(2)
若关于x的一元二次方程  的判别式
的判别式  .求证:当
.求证:当  时,二次函数
时,二次函数  的图像与x轴没有交点.
(3)
若
的图像与x轴没有交点.
(3)
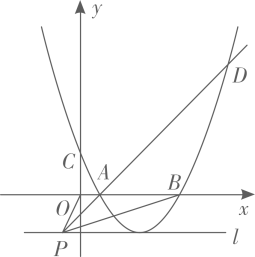
若  ,点P的坐标为
,点P的坐标为  ,过点P作直线l垂直于y轴,且抛物线的
,过点P作直线l垂直于y轴,且抛物线的  顶点在直线l上,连接OP、AP、BP,PA的延长线与抛物线
顶点在直线l上,连接OP、AP、BP,PA的延长线与抛物线  交于点D,若
交于点D,若  ,求
,求  的最小值.
的最小值.
【考点】
一元二次方程的根与系数的关系(韦达定理);
待定系数法求二次函数解析式;
二次函数图象与坐标轴的交点问题;
相似三角形的判定与性质;
二次函数y=ax²+bx+c的性质;

