0 返回出卷网首页
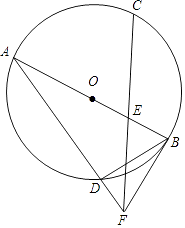
1. 如图，AB是⊙O的直径，弦AC与BD交于点E，且AC＝BD，连接AD，BC.

(1) 求证：△ADB≌△BCA；
(2) 若OD⊥AC，AB＝4，求弦AC的长；
(3) 在（2）的条件下，延长AB至点P，使BP＝2，连接PC.求证：PC是⊙O的切线.
【考点】
全等三角形的判定与性质; 等边三角形的判定与性质; 垂径定理; 圆周角定理; 切线的判定;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 困难
能力提升
换一批
1. 如图，⊙O的半径为1，A，P，B，C是⊙O上的四个点，∠APC=∠CPB=60°．

(1) 判断△ABC的形状： ；
(2) 试探究线段PA，PB，PC之间的数量关系，并证明你的结论；
(3) 当点P位于的什么位置时，四边形APBC的面积最大？求出最大面积．
综合题 普通
2. 如图，已知P是⊙O外一点，PO交圆O于点C，OC=CP=2，弦AB⊥OC，劣弧AB的度数为120°，连接PB．

(1) 求BC的长；
(2) 求证：PB是⊙O的切线．
综合题 普通
3. 如图，AB是⊙O的直径， ，E是OB的中点，连接CE并延长到点F，使EF=CE．连接AF交⊙O于点D，连接BD，BF．

(1) 求证：直线BF是⊙O的切线；
(2) 若OB=2，求BD的长．
综合题 普通