0 返回出卷网首页
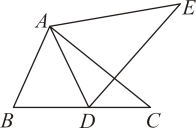
1. 在△ABC中，∠B+∠ACB＝30°，AB＝4，△ABC逆时针旋转一定角度后与△ADE重合，且点C恰好成为AD中点，如图

(1) 指出旋转中心，并求出旋转角的度数．
(2) 求出∠BAE的度数和AE的长．
【考点】
三角形内角和定理; 旋转的性质;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1. 如图，在△ABC中，∠ABC=42°，∠EAD=20°，AD是BC边上的高，AE平分∠BAC．

(1) 求∠BAC的度数；
(2) 求∠DAC的度数．
综合题 普通
2. 综合题。
(1) 已知如图1，锐角△ABC中，AB、AC边上的高CE、BD相交于O点．若∠A=70°，则∠BOC．

(2) 若将（1）题中已知条件“锐角△ABC”改为“钝角△ABC，∠A为钝角且∠A=n°”，其它条件不变（图2），请你求出∠BOC的度数．

综合题 普通
3. 在数学学习中整体思想与转化思想是我们常用到的数学思想．如图（1）中，求∠A+∠B+∠C+∠D+∠E的度数等于多少时，我们可以连接CD，利用三角形的内角和则有∠B+∠E=∠ECD+∠BDC，这样∠A、∠B、∠C、∠D、∠E的和就转化到同一个△ACD中，即∠A+∠B+∠C+∠D+∠E=180°．

尝试练习：

图（2）中∠A+∠B+∠C+∠D+∠E的度数等于．

图（3）中∠A+∠B+∠C+∠D+∠E的度数等于．

图（4）中∠A+∠B+∠C+∠D+∠E+∠F的度数等于．
综合题 普通