已知抛物线C1：y=ax2+bx+（a≠0）经过点A（﹣1，0）和B（3，0）．

0 返回出卷网首页

1. 已知抛物线C₁：y=ax²+bx+ $\text{[math]}$ （a≠0）经过点A（﹣1，0）和B（3，0）．

(1) 求抛物线C₁的解析式，并写出其顶点C的坐标；

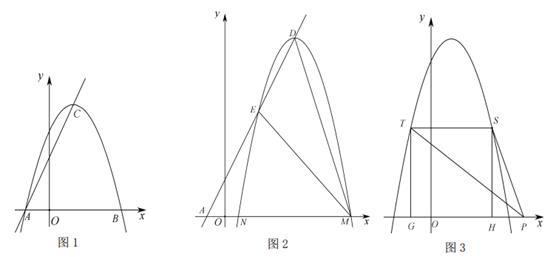
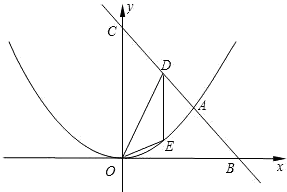
(2) 如图1，把抛物线C₁沿着直线AC方向平移到某处时得到抛物线C₂ ，此时点A，C分别平移到点D，E处．设点F在抛物线C₁上且在x轴的下方，若△DEF是以EF为底的等腰直角三角形，求点F的坐标；

(3) 如图2，在（2）的条件下，设点M是线段BC上一动点，EN⊥EM交直线BF于点N，点P为线段MN的中点，当点M从点B向点C运动时：①tan∠ENM的值如何变化？请说明理由；②点M到达点C时，直接写出点P经过的路线长．

【考点】

待定系数法求一次函数解析式; 待定系数法求二次函数解析式; 勾股定理的应用; 相似三角形的判定与性质; 等腰直角三角形;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，在平面直角坐标系中，O是坐标原点，点A的坐标是（﹣4，0），点B的坐标是（0，b）（b＞0）．P是直线AB上的一个动点，作PC⊥x轴，垂足为C．记点P关于y轴的对称点为P′（点P′不在y轴上），连接PP′，P′A，P′C．设点P的横坐标为a．

(1) 当b=3时，

①求直线AB的解析式；

②若点P′的坐标是（﹣1，m），求m的值；

(2) 若点P在第一象限，记直线AB与P′C的交点为D．当P′D：DC=1：3时，求a的值；

(3) 是否同时存在a，b，使△P′CA为等腰直角三角形？若存在，请求出所有满足要求的a，b的值；若不存在，请说明理由．

综合题困难

如图1，抛物线C₁： $\text{[math]}$ 与x轴交于A(－1，0)，B(3，0)两点，且顶点为C，直线y=kx+2经过A，C两点．

(1) 求直线AC的表达式与抛物线C₁的表达式；

(2) 如图2，将抛物线C₁沿射线AC方向平移一定距离后，得到抛物线为C₂ ，其顶点为D，抛物线C₂与直线y=kx+2的另一交点为E，与x轴交于M，N两点(M点在N点右边)，若 $\text{[math]}$ ，求点D的坐标；

(3) 如图3，若抛物线C₁向上平移4个单位得到抛物线C₃ ，正方形GHST的顶点G，H在x轴上，顶点S，T在x轴上方的抛物线C₃上，P（m，0）是射线GH上一动点，则正方形GHST的边长为，当m=时， $\text{[math]}$ 有最小值．

综合题困难

3. 如图，二次函数图象的顶点为坐标系原点O ，且经过点 $\text{[math]}$ ，一次函数的图象经过点A和点 $\text{[math]}$ ．

(1) 求二次函数与一次函数的解析式；

(2) 如果一次函数图象与y轴相交于点C ，点D在线段AC上，与y轴平行的直线DE与二次函数图象相交于点E ， $\text{[math]}$ ，求点D的坐标；

(3) 当点D在直线AC上的一个动点时，以点O、C、D、E为顶点的四边形能成为平行四边形吗？请说明理由．

综合题普通