如图，AD为△ABC的高，E为AC上一点，BE交AD于F，且有BF=AC， FD=CD。求证：

0 返回出卷网首页

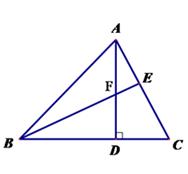
1. 如图，AD为△ABC的高，E为AC上一点，BE交AD于F，且有BF=AC， FD=CD。

求证：

(1) Rt△BDF≌Rt△ADC

(2) BE⊥AC

【考点】

全等三角形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

如图，在正方形ABCD中，点E是BC的中点，将△ABE沿AE折叠后得到△AFE，点F在正方形ABCD的内部，延长AF交CD于点G．

(1) 猜想并证明线段GF与GC的数量关系；

(2) 若将图1中的正方形改成矩形，其它条件不变，如图2，那么线段GF与GC之间的数量关系是否改变？请证明你的结论；

(3) 若将图1中的正方形改成平行四边形，其它条件不变，如图3，那么线段GF与GC之间的数量关系是否会改变？请证明你的结论．

综合题普通

2. 如图，在正方形ABCD中，点E ， F在对角线BD上，若再添加一个条件，就可证出AE=CF ．

(1) 你添加的条件是

(2) 请你根据题目中的条件和你添加的条件证明AE=CF ．

综合题普通

3. 如图，点A是线段DE上一点，∠BAC=90°，AB=AC，BD⊥DE，CE⊥DE.

(1) 求证：DE=BD+CE.

(2) 如果是如图2这个图形，BD、CE、DE有什么数量关系？并证明.

综合题普通