1.
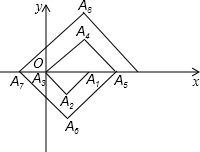
如图,点P在平面直角坐标系中按图中箭头所示的方向运动,每次运动一个单位,△A3A4A5和△A8A9A10都是等边三角形.第一次从(0,1)运动到点A1(0,2),第二次接着运动到点A2(1,2),第三次运动到点A3(1,1),…,经过2019次运动,动点P所在位置A2019的坐标是( )

A.
(807,  )
B.
(
)
B.
(  ,2﹣
,2﹣  )
C.
(
)
C.
(  ,
,  )
D.
(807,2﹣
)
D.
(807,2﹣  )
)
【考点】
坐标与图形性质;
探索图形规律;