1.
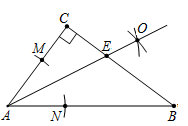
如图,在△ABC中,∠C=90°,AC=8,BC=6,按下列步骤作图:①以点A为圆心,适当长为半径画弧,分别交AC,AB于点D,E;②分别以D,E为圆心,DE的长为半径画弧,两弧相交于点F;③作射线AF,交BC于点G,则CG=( )

A.
3
B.
6
C.
 D.
D.

【考点】
全等三角形的判定与性质;
角平分线的性质;
勾股定理;
基础巩固
能力提升
变式训练
拓展培优
真题演练