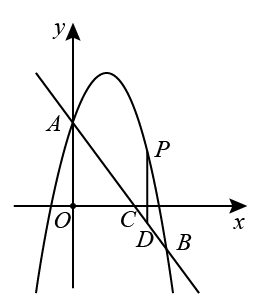
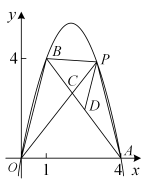
如图，在平面直角坐标系xOy中，抛物线y＝ x2+mx+n经过点B（6，1），C（5，0），且与y轴交于点A ．

0 返回出卷网首页

1. 如图，在平面直角坐标系xOy中，抛物线y＝ $\text{[math]}$ x²+mx+n经过点B（6，1），C（5，0），且与y轴交于点A ．

(1) 求抛物线的表达式及点A的坐标；

(2) 点P是y轴右侧抛物线上的一点，过点P作PQ⊥OA ，交线段OA的延长线于点Q ，如果∠PAB＝45°．求证：△PQA∽△ACB；

(3) 若点F是线段AB（不包含端点）上的一点，且点F关于AC的对称点F′恰好在上述抛物线上，求FF′的长．

【考点】

待定系数法求二次函数解析式; 相似三角形的判定与性质; 二次函数与一次函数的综合应用;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，在平面直角坐标系中，已知直线 $\text{[math]}$ 与x轴交于点A、与y轴交于点B，抛物线 $\text{[math]}$ 经过点A、B．

(1) 求抛物线的表达式；

(2) P是抛物线上一点，且位于直线 $\text{[math]}$ 上方，过点P作 $\text{[math]}$ 轴、 $\text{[math]}$ 轴，分别交直线 $\text{[math]}$ 于点M、N．

①当 $\text{[math]}$ 时，求点P的坐标；

②连接 $\text{[math]}$ 交 $\text{[math]}$ 于点C，当点C是 $\text{[math]}$ 的中点时，求 $\text{[math]}$ 的值．

综合题困难

2. 已知抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于 $\text{[math]}$ 和 $\text{[math]}$ 两点，与 $\text{[math]}$ 轴交于 $\text{[math]}$ 点，且 $\text{[math]}$ .对于该抛物线上的任意两点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，当 $\text{[math]}$ 时，总有 $\text{[math]}$ .

(1) 求抛物线的解析式；

(2) 若过点 $\text{[math]}$ 的直线 $\text{[math]}$ 与该抛物线交于另一点E，与线段BC交于点 $\text{[math]}$ .作 $\text{[math]}$ ，EG与BC交于 $\text{[math]}$ 点，求 $\text{[math]}$ 的最大值，并求此时 $\text{[math]}$ 点的坐标；

(3) 若直线 $\text{[math]}$ 与抛物线交于 $\text{[math]}$ ， $\text{[math]}$ 两点 $\text{[math]}$ ， $\text{[math]}$ 不与 $\text{[math]}$ ， $\text{[math]}$ 重合），直线 $\text{[math]}$ ， $\text{[math]}$ 分别与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ， $\text{[math]}$ ，设 $\text{[math]}$ ， $\text{[math]}$ 两点的纵坐标分别为 $\text{[math]}$ ， $\text{[math]}$ ，试探究 $\text{[math]}$ 、 $\text{[math]}$ 之间的数量关系.

综合题困难

3. 如图，抛物线y＝﹣ $\text{[math]}$ x²+bx+c与x轴交于点A（4，0），与y轴交于点B，且OA=OB，在x轴上有一动点D（m，0）（0＜m＜4），过点D作x轴的垂线交直线AB于点C，交抛物线于点E，

(1) 求抛物线的函数表达式.

(2) 当点C是DE的中点时，求出m的值.

(3) 在（2）的条件下，将线段OD绕点O逆时针旋转得到OD′，旋转角为α（0°＜a＜90°），连接D′A、D′B，直接写出D′A+ $\text{[math]}$ D′B的最小值.

综合题困难