1.
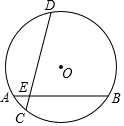
如图,⊙O直径AB和弦CD相交于点E , AE=2,EB=6,∠DEB=30°,求弦CD长.

【考点】
含30°角的直角三角形;
勾股定理;
垂径定理;
基础巩固
能力提升
变式训练
拓展培优
真题演练