1.
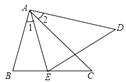
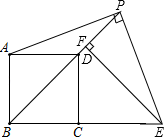
已知△ABC为等腰直角三角形,∠ACB=90°,点P在BC边上(P不与B、C重合)或点P在△ABC内部,连接CP、BP,将CP绕点C逆时针旋转90°,得到线段CE;将BP绕点B顺时针旋转90°,得到线段BD,连接ED交AB于点O.
(1)如图a,当点P在BC边上时,求证:OA=OB;
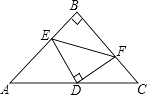
(2)如图b,当点P在△ABC内部时,
①OA=OB是否成立?请说明理由;
②直接写出∠BPC为多少度时,AB=DE.

【考点】
全等三角形的判定与性质;
等腰直角三角形;
基础巩固
能力提升
变式训练
拓展培优
真题演练