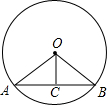
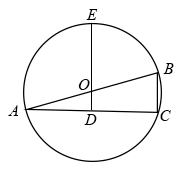
如图，⊙O的半径是， △ABC是⊙O的内接三角形，过圆心O分别作AB，BC，AC的垂线，垂足为E，F，G，连接EF，若OG=1，则EF的长为．

0 返回出卷网首页

1. 如图，⊙O的半径是 $\text{[math]}$ ， △ABC是⊙O的内接三角形，过圆心O分别作AB，BC，AC的垂线，垂足为E，F，G，连接EF，若OG=1，则EF的长为．

【考点】

勾股定理; 垂径定理; 三角形的中位线定理;

【答案】

您现在未登录，无法查看试题答案与解析。登录

填空题普通

1. 《九章算术》是中国传统数学重要的著作之一，其中第九卷《勾股》中记载了一个“圆材埋壁”的问题：“今有圆材，埋在壁中，不知大小．以锯锯之、深一寸，锯道长一尺，问径几何？”用几何语言表达为：如图， $\text{[math]}$ 是 $\text{[math]}$ 的直径，弦 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 寸， $\text{[math]}$ 寸，则半径 $\text{[math]}$ 长为寸．

填空题容易

2. 如图，已知在半径为10的⊙O中，弦AB=16，OC⊥AB ，则OC的长为.

填空题容易

3. 如图， $\text{[math]}$ 的弦AB和直径CD交于点E，且CD平分AB，已知AB=8，CE=2，那么 $\text{[math]}$ 的半径长是．

填空题容易