1.
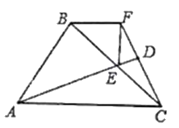
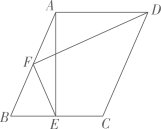
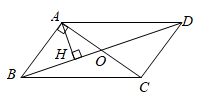
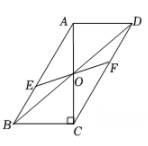
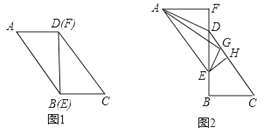
如图1,在平行四边形ABCD中,连接BD,AD=6cm,BD=8cm,∠DBC=90°,现将△AEF沿BD的方向匀速平移,速度为2cm/s,同时,点G从点D出发,沿DC的方向匀速移动,速度为2cm/s.当△AEF停止移动时,点G也停止运动,连接AD,AG,EG,过点E作EH⊥CD于点H,如图2所示,设△AEF的移动时间为t(s)(0<t<4).
(1)当t=1时,求EH的长度;
(2)若EG⊥AG,求证:EG2=AE•HG;
(3)设△AGD的面积为y(cm2),当t为何值时,y可取得最大值,并求y的最大值.
【考点】
勾股定理;
平行四边形的性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练