已知Rt△ABC中，∠B=90°，AC=20，AB=10，P是边AC上一点（不包括端点A、C），过点P作PE⊥BC于点E，过点E作EF∥AC，交AB于点F．设PC=x，PE=y．

0 返回出卷网首页

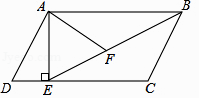
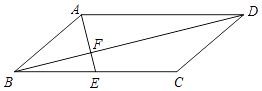
1. 已知Rt△ABC中，∠B=90°，AC=20，AB=10，P是边AC上一点（不包括端点A、C），过点P作PE⊥BC于点E，过点E作EF∥AC，交AB于点F．设PC=x，

PE=y．

(1) 求y与x的函数关系式；

(2) 是否存在点P使△PEF是Rt△？若存在，求此时的x的值；若不存在，请说明理由．

【考点】

平行四边形的性质; 矩形的性质; 相似三角形的判定与性质; 解直角三角形;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，在Rt△ABC中，∠ACB=90°，AC=8cm，AB=10cm．点P从点A出发，以5cm/s的速度从点A运动到终点B；同时，点Q从点C出发，以3cm/s的速度从点C运动到终点B，连结PQ；过点P作PD⊥AC交AC于点D，将△APD沿PD翻折得到△A′PD，以A′P和PB为邻边作▱A′PBE，A′E交射线BC于点F，交射线PQ于点G．设▱A′PBE与四边形PDCQ重叠部分图形的面积为Scm² ，点P的运动时间为ts．

(1) 当t为何值时，点A′与点C重合；

(2) 用含t的代数式表示QF的长；

(3) 求S与t的函数关系式；

(4) 请直接写出当射线PQ将▱A′PBE分成的两部分图形的面积之比是1：3时t的值．

综合题困难

2. 如图，在▱ABCD中过点A作AE⊥DC，垂足为E，连接BE，F为BE上一点，且∠AFE=∠D．

(1) 求证：△ABF∽△BEC；

(2) 若AD=5，AB=8，sinD= $\text{[math]}$ ，求AF的长．

综合题普通

3. 如图，在平行四边形ABCD中，点E为BC的中点，AE与对角线BD交于点F．

(1) 求证：DF=2BF；

(2) 当∠AFB=90°且tan∠ABD= $\text{[math]}$ 时，若CD= $\text{[math]}$ ，求AD长．

综合题普通