已知直角三角形纸片的两条直角边长分别为m和n（m＜n），过锐角顶点把该纸片剪成两个三角形，若这两个三角形都为等腰三角形，则（）

0 返回出卷网首页

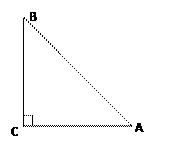
1. 已知直角三角形纸片的两条直角边长分别为m和n（m＜n），过锐角顶点把该纸片剪成两个三角形，若这两个三角形都为等腰三角形，则（）

A. m²+2mn+n²=0 B. m²﹣2mn+n²=0 C. m²+2mn﹣n²=0 D. m²﹣2mn﹣n²=0

【考点】

等腰三角形的性质; 等腰直角三角形;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题普通

1. 如图，AD，CE分别是△ABC的中线和角平分线．若AB=AC，∠CAD=20°，则∠ACE的度数是（）

A. 20° B. 35° C. 40° D. 70°

单选题容易

2. 等腰三角形的一个内角为 $\text{[math]}$ ，则另外两个内角的度数分别是（）

A. $\text{[math]}$ B. $\text{[math]}$ 或 $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$ 或 $\text{[math]}$

单选题容易

3. 方程x²﹣9x+14＝0的两个根分别是等腰三角形的底和腰，则这个三角形的周长为（）

A. 11 B. 16 C. 11或16 D. 不能确定

单选题容易