0 返回出卷网首页
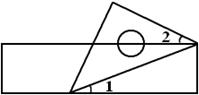
1. 如图，△ABC和△DEC都是等腰直角三角形，C为它们的公共直角顶点，连AD，BE，F为线段AD的中点，连接CF

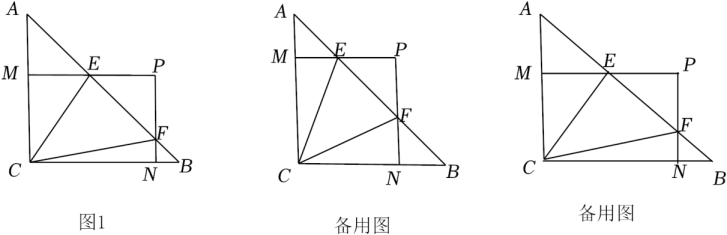
(1) 如图1，当D点在BC上时，求证：①BE=2CF，②BE⊥CF．
(2) 如图2，把△DEC绕C点顺时针旋转一个锐角，其他条件不变，问（1）中的关系是否仍然成立？如果成立请证明．如果不成立，请写出相应的正确的结论并加以证明．
【考点】
等腰直角三角形;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1. 如图，抛物线y=ax2+c（a≠0）与y轴交于点A，与x轴交于点B，C两点（点C在x轴正半轴上），△ABC为等腰直角三角形，且面积为4．现将抛物线沿BA方向平移，平移后的抛物线经过点C时，与x轴的另一交点为E，其顶点为F，对称轴与x轴的交点为H．

(1) 求a，c的值；
(2) 连结OF，试判断△OEF是否为等腰三角形，并说明理由；
(3) 现将一足够大的三角板的直角顶点Q放在射线AF或射线HF上，一直角边始终过点E，另一直角边与y轴相交于点P，是否存在这样的点Q，使以点P，Q，E为顶点的三角形与△POE全等？若存在，直接写出点Q的坐标；若不存在，请说明理由．
综合题 普通
2. 如图1，△ABC和△CDE都是等腰直角三角形，∠C=90°，将△CDE绕点C逆时针旋转一个角度α（0°＜α＜90°），使点A，D，E在同一直线上，连接AD，BE．

(1) ①依题意补全图2；

②求证：AD=BE，且AD⊥BE；

③作CM⊥DE，垂足为M，请用等式表示出线段CM，AE，BE之间的数量关系；
(2) 如图3，正方形ABCD边长为 ，若点P满足PD=1，且∠BPD=90°，请直接写出点A到BP的距离．
综合题 普通
3. 如图，图1和图2都是7×4正方形网格，每个小正方形的边长为l，请按要求画出下列图形，所画图形的各个顶点均在所给小正方形的顶点上．

(1) 在图1中画出一个等腰直角三角形ABC；
(2) 在图2中画出一个钝角三角形ABD，使△ABD的面为3.

综合题 普通