1.
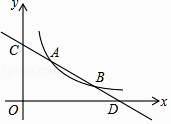
如图，在平面直角坐标系xOy中，直线y=﹣x+3与x轴交于点C，与直线AD交于点A（ 
， 
），点D的坐标为（0，1）
(1)
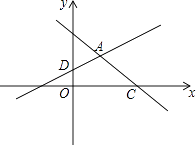
求直线AD的解析式；
(2)
直线AD与x轴交于点B，若点E是直线AD上一动点（不与点B重合），当△BOD与△BCE相似时，求点E的坐标．
【考点】
待定系数法求一次函数解析式;
相似三角形的性质;
