1.
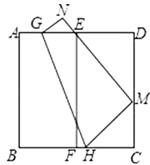
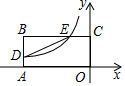
如图,矩形EFGH的四个顶点分别在矩形ABCD的各条边上,AB=EF,FG=2,GC=3.有以下四个结论:①∠BGF=∠CHG;②△BFG≌△DHE;③tan∠BFG=  ;④矩形EFGH的面积是4
;④矩形EFGH的面积是4  .其中一定成立的是.(把所有符合题意结论的序号填在横线上)
.其中一定成立的是.(把所有符合题意结论的序号填在横线上)

【考点】
全等三角形的判定与性质;
勾股定理;
相似三角形的判定与性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练