1.
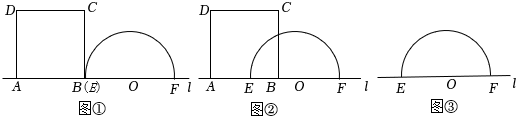
如图1,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,点B.C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.

(1)
当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明,若不成立,请说明理由.
(2)
当△ABC绕点A逆时针旋转45°时,如图3,延长BD交CF于点H.
①探究BD与CF之间的位置关系,并说明理由;
②当AB= ,AD=
+1时,求线段DH的长.
【考点】
三角形全等的判定;
勾股定理;