1.
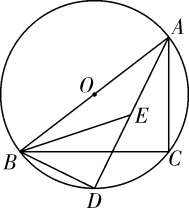
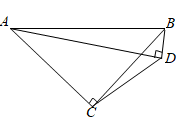
如图,△ABC内接于⊙O , AB是⊙O的直径,CE平分∠ACB交⊙O于E , 交AB于点D , 连接AE , ∠AEC=30°,AC=5.

(1)
求CE的长;
(2)
求S△ADC:S△ACE的比值.
【考点】
勾股定理;
圆周角定理;
等腰直角三角形;
能力提升
真题演练