1.
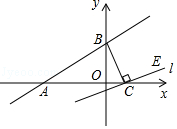
在平面直角坐标系中,  是坐标原点,直线
是坐标原点,直线  分别交
分别交  轴,
轴,  轴于
轴于  、
、  两点.
两点.

(1)
求直线  的解析式;
(2)
点
的解析式;
(2)
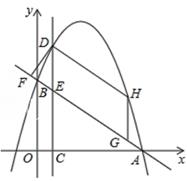
点  为直线
为直线  上一动点,以
上一动点,以  为顶点的抛物线
为顶点的抛物线  与直线
与直线  的另一交点为
的另一交点为  (如图1),连
(如图1),连  、
、  ,在点
,在点  的运动过程中
的运动过程中  的面积
的面积  是否变化,若变化,求出
是否变化,若变化,求出  的范围;若不变,求出
的范围;若不变,求出  的值;
(3)
平移(2)中的抛物线,使顶点为
的值;
(3)
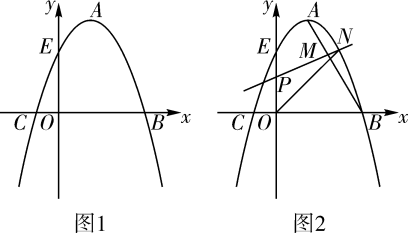
平移(2)中的抛物线,使顶点为  ,抛物线与
,抛物线与  轴的正半轴交于点
轴的正半轴交于点  (如图2) ,
(如图2) ,  ,
,  为抛物线上两点,若以
为抛物线上两点,若以  为直径的圆经过点
为直径的圆经过点  ,求直线
,求直线  经过的定点
经过的定点  的坐标.
的坐标.
【考点】
待定系数法求一次函数解析式;
相似三角形的判定与性质;
二次函数与一次函数的综合应用;