1.
根据题意解答

(1)
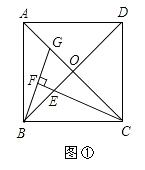
如图1,已知E是矩形ABCD的边AB上一点,EF⊥DE交BC于点F,证明:△ADE∽△BFE.
(2)
这个相似的基本图形像字母K,可以称为“K”型相似,但更因为图形的结构特征是一条线上有3个垂直关系,也常被称为“一线三垂直”,那普通的3个等角又会怎样呢?
(3)
变式二如图4,隐藏变式1图形中的线段AE,在得到的新图形中.
(4)
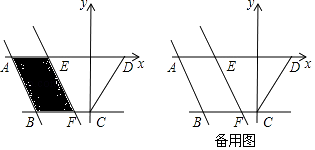
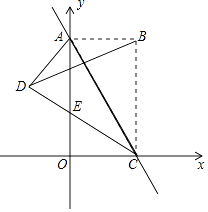
交式三已知,相邻两条平形直线间的距离相等,若等腰直角△ABC的三个顶点分别在这三条平行直线上,则cosa的值是(直接写出结果).
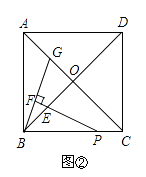
变式一如图2,已知等边三角形ABC,点D、E分别为BC,AC上的点,∠ADE=60°.
①图中有相似三角形吗?请说明理由.
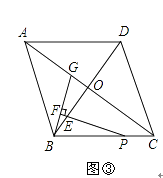
②如图3,若将∠ADE在△ABC的内部(∠ADE两边不与BC重合),绕点D逆时针旋转一定的角度,还有相似三角形吗?
①如果∠B=∠C=∠ADE=50°,图中有相似三角形吗?请说明理由.
②如图5,若∠B=∠C=∠ADE=∠a,∠a为任意角,还有相似三角形吗?
【考点】
全等三角形的应用;
相似三角形的应用;
能力提升
真题演练