1.
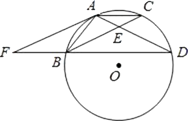
已知：如图，以矩形ABCD的对角线AC的中点O为圆心，OA长为半径作⊙O，⊙O经过B、D两点，过点B作BK⊥AC，垂足为K．过D作DH∥KB，DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H．
(1)
求证：AE=CK；
(2)
如果AB=a，AD= 
（a为大于零的常数），求BK的长：
(3)
若F是EG的中点，且DE=6，求⊙O的半径和GH的长．
【考点】
全等三角形的判定与性质;
垂径定理;
相似三角形的判定与性质;
三角形的中位线定理;
