如图，点E、F分别为菱形ABCD边AD、CD的中点.

0 返回出卷网首页

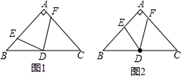
1. 如图，点E、F分别为菱形ABCD边AD、CD的中点.

(1) 求证：BE=BF；

(2) 当△BEF为等边三角形时，求证：∠D=2∠A.

【考点】

全等三角形的判定与性质; 相似三角形的判定与性质; 三角形的中位线定理;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 已知，如图1，AD是△ABC的角平分线，且AD=BD，

(1) 求证：△CDA∽△CAB；

(2) 若AD=6，CD=5，求AC的值；

(3) 如图2，延长AD至E，使AE=AB，过E点作EF∥AB，交AC于点F，试探究线段EF与线段AD的大小关系．

综合题普通

2. 已知 $\text{[math]}$ 是一段圆弧上的两点，且在直线 $\text{[math]}$ 的同侧，分别过这两点作 $\text{[math]}$ 的垂线，垂足为 $\text{[math]}$ 是 $\text{[math]}$ 上一动点，连接 $\text{[math]}$ ，且 $\text{[math]}$ .

(1) 如图①，如果 $\text{[math]}$ ，且 $\text{[math]}$ ，求 $\text{[math]}$ 的长；

(2) 如图②，若点 $\text{[math]}$ 恰为这段圆弧的圆心，则线段 $\text{[math]}$ 之间有怎样的等量关系?请写出你的结论并予以证明.再探究：当 $\text{[math]}$ 分别在直线 $\text{[math]}$ 两侧且 $\text{[math]}$ ，而其余条件不变时，线段 $\text{[math]}$ 之间又有怎样的等量关系?请直接写出结论，不必证明.

综合题普通

3. 已知：△ABC，AB=AC，∠BAC=90°，点D是边BC的中点，点E在边AB上(点E不与点A、B重合)，点F在边AC上，联结DE、DF．

(1) 如图1，当∠EDF=90°时，求证：BE=AF；

(2) 如图2，当∠EDF=45°时，求证： $\text{[math]}$ ．

综合题普通