1.
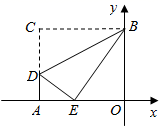
已知:如图,点E是矩形ABCD的边AD上一点,BE=AD,AE=8,现有甲乙二人同时从E点出发,分别沿EC、ED方向前进,甲的速度是乙的  倍,甲到达点目的地C点的同时乙恰巧到达终点D处.
倍,甲到达点目的地C点的同时乙恰巧到达终点D处.

(1)
求tan∠ECD的值
(2)
求线段AB及BC的长度.
【考点】
勾股定理;
矩形的性质;
锐角三角函数的定义;
能力提升
真题演练