【问题情境】已知矩形的面积为a（a为常数，a＞0），当该矩形的长为多少时，它的周长最小？最小值是多少？【数学模型】设该矩形的长为x，周长为y，则y与x的函数关系式为y=2（x+ ）（x＞0）．【探索研究】

1. 【问题情境】

已知矩形的面积为a（a为常数，a＞0），当该矩形的长为多少时，它的周长最小？最小值是多少？

【数学模型】

设该矩形的长为x，周长为y，则y与x的函数关系式为y=2（x+ $\text{[math]}$ ）（x＞0）．

【探索研究】

(1) 我们可以借鉴以前研究函数的经验，先探索函数y=x+ $\text{[math]}$ （x＞0）的图象和性质．

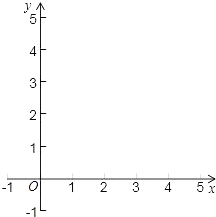
①填写下表，画出函数的图象；

x	…	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	1	2	3	4	…
y	…								…

②观察图象，写出该函数两条不同类型的性质；

③在求二次函数y=ax²+bx+c（a≠0）的最大（小）值时，除了通过观察图象，还可以通过配方得到．请你通过配方求函数y=x+ $\text{[math]}$ （x＞0）的最小值．

(2) 用上述方法解决“问题情境”中的问题，直接写出答案．

【考点】

完全平方公式及运用; 反比例函数的性质; 二次函数的最值; 一次函数的性质; 配方法的应用;

【答案】

您现在未登录，无法查看试题答案与解析。登录

实践探究题普通

证明：设点 $\text{[math]}$ 在正比例函数 $\text{[math]}$ 的图象上，且 $\text{[math]}$ ，

$\text{[math]}$ ，

$\text{[math]}$

$\text{[math]}$ $\text{[math]}$

$\text{[math]}$ $\text{[math]}$ $\text{[math]}$

$\text{[math]}$ 随着 $\text{[math]}$ 的增大而增大．

实践探究题普通

已知矩形的面积为a（a为常数，a＞0），当该矩形的长为多少时，它的周长最小？最小值是多少？

【数学模型】

设该矩形的长为x，周长为y，则y与x的函数表达式为y=2（x+ $\text{[math]}$ ）（x＞0）．

【探索研究】

小彬借鉴以前研究函数的经验，先探索函数y=x+ $\text{[math]}$ 的图象性质．

x	…	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	1	2	3	m	…
y	…	4 $\text{[math]}$	3 $\text{[math]}$	2 $\text{[math]}$	2	2 $\text{[math]}$	3 $\text{[math]}$	4 $\text{[math]}$	…

① 写出m的值；

②画出该函数图象，结合图象，得出当x=时，y有最小值，y_最小=；

提示：在求二次函数y=ax²+bx+c（a≠0）的最大（小）值时，除了通过观察图象，还可以通过配方得到．试用配方法求函数y=x+ $\text{[math]}$ （x＞0）的最小值，解决问题（2）

直接写出“问题情境”中问题的结论．

实践探究题普通

解：设 $\text{[math]}$ ，则 $\text{[math]}$ $\text{[math]}$ ．

所以 $\text{[math]}$ $\text{[math]}$ ．

请仿照上例解决下面的问题：

实践探究题普通