1.
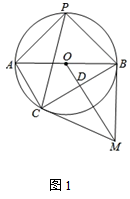
如图1，AB是⊙O的直径，点P在⊙O上，且PA=PB，点M是⊙O外一点，MB与⊙O相切于点B，连接OM，过点A作AC∥OM交⊙O于点C，连接BC交OM于点D.
(1)
填空：OD=AC；求证：MC是⊙O的切线；
(2)
若OD=9，DM=16，连接PC，求sin∠APC的值；
(3)
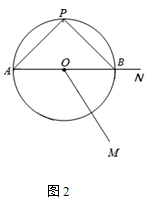
如图2，在（2）的条件下，延长OB至N，使BN= 
，在⊙O上找一点Q，使得 
的值最小，请直接写出其最小值为.
【考点】
全等三角形的判定与性质;
切线的判定与性质;
相似三角形的判定与性质;
锐角三角函数的定义;
三角形的中位线定理;
