1.
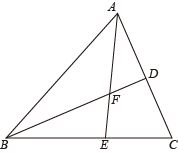
如图,在  中,按以下步骤作图:
中,按以下步骤作图:
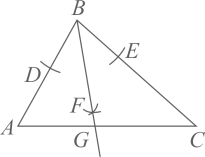
①以点B为圆心,任意长为半径作弧,分别交AB、BC于点D、E.
②分别以点D、E为圆心,大于 的同样长为半径作弧,两弧交于点F.
③作射线BF交AC于点G.
如果 ,
,
的面积为18,则
的面积为.
【考点】
三角形的面积;
角平分线的性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练