如图，在平行四边形ABCD中，AE，CF分别平分∠BAD和∠DCB，交对角线BD于点E，F.

0 返回出卷网首页

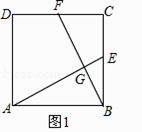
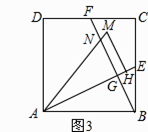
1. 如图，在平行四边形ABCD中，AE，CF分别平分∠BAD和∠DCB，交对角线BD于点E，F.

(1) 若∠BCF＝60°，求∠ABC的度数；

(2) 求证：BE＝DF.

【考点】

三角形全等及其性质; 平行四边形的性质; 三角形全等的判定-ASA;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 在直线 $\text{[math]}$ 上（ $\text{[math]}$ 、 $\text{[math]}$ 之间不能直接测量），点 $\text{[math]}$ 、 $\text{[math]}$ 在 $\text{[math]}$ 异侧，测得 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．

(1) 求证： $\text{[math]}$ ；

(2) 若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长度．

综合题普通

2. 在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点F是射线 $\text{[math]}$ 上一点，连接 $\text{[math]}$ ，过点C作 $\text{[math]}$ ，垂足为点E，直线 $\text{[math]}$ 、 $\text{[math]}$ 相交于点D．

(1) 如图1所示，当点F在线段 $\text{[math]}$ 延长线上时，求证： $\text{[math]}$ ≌ $\text{[math]}$ ；

(2) 如图2所示，当点F在线段 $\text{[math]}$ 上时，连接 $\text{[math]}$ ，过点A作 $\text{[math]}$ 于M， $\text{[math]}$ 于N，求证： $\text{[math]}$ 平分 $\text{[math]}$ ．

综合题困难

3. 如图1，在正方形ABCD中，E、F分别为BC、CD的中点，连接AE、BF，交点为G．

(1) 求证：AE⊥BF；

(2) 将△BCF沿BF对折，得到△BPF（如图2），延长FP到BA的延长线于点Q，求sin∠BQP的值；

(3) 将△ABE绕点A逆时针方向旋转，使边AB正好落在AE上，得到△AHM（如图3），若AM和BF相交于点N，当正方形ABCD的面积为4时，求四边形GHMN的面积．

综合题普通