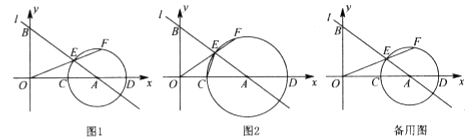
如图（1）放置两个全等的含有30°角的直角三角板与，若将三角板向右以每秒1个单位长度的速度移动（点C与点E重合时移动终止），移动过程中始终保持点B、F、C、E在同一条直线上，如图（2），与、分别交于点P、M，与交于点Q，其中，设三角板移动时间为x秒.

0 返回出卷网首页

1. 如图（1）放置两个全等的含有30°角的直角三角板 $\text{[math]}$ 与 $\text{[math]}$ ，若将三角板 $\text{[math]}$ 向右以每秒1个单位长度的速度移动（点C与点E重合时移动终止），移动过程中始终保持点B、F、C、E在同一条直线上，如图（2）， $\text{[math]}$ 与 $\text{[math]}$ 、 $\text{[math]}$ 分别交于点P、M， $\text{[math]}$ 与 $\text{[math]}$ 交于点Q，其中 $\text{[math]}$ ，设三角板 $\text{[math]}$ 移动时间为x秒.

(1) 在移动过程中，试用含x的代数式表示 $\text{[math]}$ 的面积；

(2) 计算x等于多少时，两个三角板重叠部分的面积有最大值？最大值是多少？

【考点】

二次函数的最值; 解直角三角形;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 一个足球被从地面向上踢出，它距地面高度y（m）可以用二次函数y=﹣4.9x²+19.6x刻画，其中x（s）表示足球被踢出后经过的时间．

(1) 解方程﹣4.9x²+19.6x=0，并说明其根的实际意义；

(2) 求经过多长时间，足球到达它的最高点？最高点的高度是多少？

综合题普通

2. 已知函数y=-x²+bx+c（b，c为常数）的图象经过点（0，﹣3），（﹣6，﹣3）．

(1) 求b，c的值．

(2) 当﹣4≤x≤0时，求y的最大值．

(3) 当m≤x≤0时，若y的最大值与最小值之和为2，求m的值．

综合题普通

3. 已知函数 $\text{[math]}$ 为常数）的图象经过点 $\text{[math]}$ ．

(1) 求 $\text{[math]}$ 满足的关系式；

(2) 设该函数图象的顶点坐标是 $\text{[math]}$ ，当 $\text{[math]}$ 的值变化时，求 $\text{[math]}$ 关于 $\text{[math]}$ 的函数解析式；

(3) 设该函数的图象不经过第三象限，当-5 $\text{[math]}$ 时，函数的最大值与最小值之差为16，求 $\text{[math]}$ 的值．

综合题普通