1.
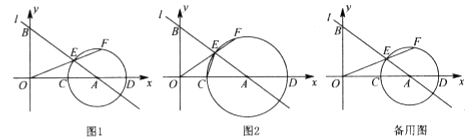
如图1,直线l:  与x轴交于点A(4,0),与y轴交于点B,点C是线段OA上一动点(0<AC<
与x轴交于点A(4,0),与y轴交于点B,点C是线段OA上一动点(0<AC<  ),以点A为圆心,AC长为半径作⊙A交x轴于另一点D,交线段AB于点E,连结OE并延长交⊙A于点F.
),以点A为圆心,AC长为半径作⊙A交x轴于另一点D,交线段AB于点E,连结OE并延长交⊙A于点F.
(1)
求直线l的函数表达式和tan∠BAO的值;
(2)
如图2,连结CE,当CE=EF时,
(3)
当点C在线段OA上运动时,求OE·EF的最大值.
①求证:△OCE∽△OEA;
②求点E的坐标;
【考点】
二次函数的最值;
相似三角形的判定与性质;
解直角三角形;
能力提升
真题演练