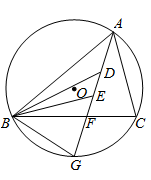
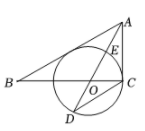
如图所示，△ABC内接于⊙O，且AB为⊙O的直径，作的平分线交圆周于点D，连结AD、BD，AB、CD交于点E.

0 返回出卷网首页

1. 如图所示，△ABC内接于⊙O，且AB为⊙O的直径，作 $\text{[math]}$ 的平分线交圆周于点D，连结AD、BD，AB、CD交于点E.

(1) 求证：△ABD为等腰直角三角形；

(2) 填空：

①若 $\text{[math]}$ ，则AE的长度为；

②在①的条件下，延长AC、DB交于点P，则 $\text{[math]}$ .

【考点】

角平分线的性质; 圆周角定理; 相似三角形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，在△ABC中，点N为AC边的任意一点，D为线段AB上一点，若∠MPN的顶点P为线段CD上任一点，其两边分别与边BC，AC交于点M、N，且∠MPN+∠ACB=180°．

(1) 如图1，若AC=BC，∠ACB=90°，且D为AB的中点时，则 $\text{[math]}$ =，请证明你的结论；

(2) 如图2，若BC=m，AC=n，∠ACB=90°，且D为AB的中点时，则 $\text{[math]}$ =；

(3) 如图3，若 $\text{[math]}$ =k，BC=m，AC=n，请直接写出 $\text{[math]}$ 的值．（用k，m，n表示）

综合题普通

2. 如图，已知线段AB∥CD，AD与BC相交于点K，E是线段AD上一动点．

(1) 若BK= $\text{[math]}$ KC，求 $\text{[math]}$ 的值；

(2) 连接BE，若BE平分∠ABC，则当AE= $\text{[math]}$ AD时，猜想线段AB、BC、CD三者之间有怎样的等量关系？请写出你的结论并予以证明．再探究：当AE= $\text{[math]}$ AD（n＞2），而其余条件不变时，线段AB、BC、CD三者之间又有怎样的等量关系？请直接写出你的结论，不必证明．

综合题普通

3. 如图，锐角三角形ABC内接于⊙O，∠BAC的平分线AG交⊙O于点G，交BC边于点F，连结BG。

(1) 求证：△ABG∽△AFC；

(2) 已知AB= $\text{[math]}$ ，AC=AF= $\text{[math]}$ ，求线段FG的长（用含 $\text{[math]}$ ， $\text{[math]}$ 的代数式表示）；

(3) 已知点E在线段AF上（不与点A，点F重合），点D在线段AE上（不与点A，点E重合），∠ABD=∠CBE，求证： $\text{[math]}$ 。

综合题困难