1.
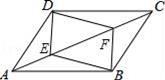
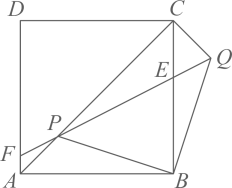
背景：一次小组合作探究课上，小明将两个正方形按背景图位置摆放（点E，A，D在同一条直线上），发现BE=DG且BE⊥DG．小组讨论后，提出了三个问题，请你帮助解答：
(1)
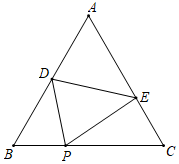
将正方形AEFG绕点A按逆时针方向旋转，（如图1）还能得到BE=DG吗？如果能，请给出证明．如若不能，请说明理由：
(2)
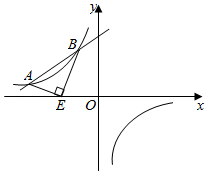
把背景中的正方形分别改为菱形AEFG和菱形ABCD，将菱形AEFG绕点A按顺时针方向旋转，（如图2）试问当∠EAG与∠BAD的大小满足怎样的关系时，背景中的结论BE=DG仍成立？请说明理由；
(3)
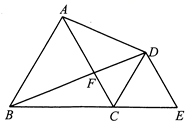
把背景中的正方形改成矩形AEFG和矩形ABCD，且 
，AE=4，AB=8，将矩形AEFG绕点A按顺时针方向旋转（如图3），连接DE，BG．小组发现：在旋转过程中， BG2+DE2是定值，请求出这个定值．
【考点】
三角形全等及其性质;
三角形全等的判定;
相似三角形的判定与性质;
