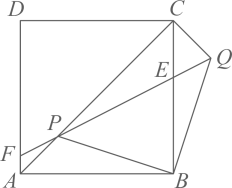
如图，正方形ABCD中，P是对角线AC上的一个动点（不与A、C重合），连结BP ，将BP绕点B顺时针旋转到BQ ，连结QP交BC于点E ， QP延长线与边AD交于点F ．

0 返回出卷网首页

1. 如图，正方形ABCD中，P是对角线AC上的一个动点（不与A、C重合），连结BP ，将BP绕点B顺时针旋转 $\text{[math]}$ 到BQ ，连结QP交BC于点E ， QP延长线与边AD交于点F ．

(1) 连结CQ ，求证： $\text{[math]}$ ；

(2) 若 $\text{[math]}$ ，求 $\text{[math]}$ 的值；

(3) 求证： $\text{[math]}$ ．

【考点】

三角形全等及其性质; 三角形全等的判定; 正方形的性质; 相似三角形的判定与性质; 旋转的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 已知：如图1，在面积为3的正方形ABCD中，E、F分别是BC和CD边上的两点，AE⊥BF于点G，且BE=1．

(1) 求证：△ABE≌△BCF；

(2) 求出△ABE和△BCF重叠部分（即△BEG）的面积；

(3) 现将△ABE绕点A逆时针方向旋转到△AB′E′（如图2），使点E落在CD边上的点E′处，问△ABE在旋转前后与△BCF重叠部分的面积是否发生了变化？请说明理由．

综合题普通

(1) 如图1，正方形 $\text{[math]}$ 与正方形 $\text{[math]}$ 有公共的顶点A，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．

①求证： $\text{[math]}$ ；

②求 $\text{[math]}$ 的值；

(2) 将图1中的正方形 $\text{[math]}$ 旋转到图2的位置，当 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 在一条直线上，若 $\text{[math]}$ ，求正方形 $\text{[math]}$ 的边长．

综合题困难

3. 如图1，已知P为正方形ABCD的对角线AC上一点（不与A、C重合），PE⊥BC于点E，PF⊥CD于点F．

(1) 求证：BP=DP；

(2) 如图2，若四边形PECF绕点C按逆时针方向旋转，在旋转过程中是否总有BP=DP？若是，请给予证明；若不是，请用反例加以说明；

(3) 试选取正方形ABCD的两个顶点，分别与四边形PECF的两个顶点连接，使得到的两条线段在四边形PECF绕点C按逆时针方向旋转的过程中长度始终相等，并证明你的结论．

综合题普通