1.
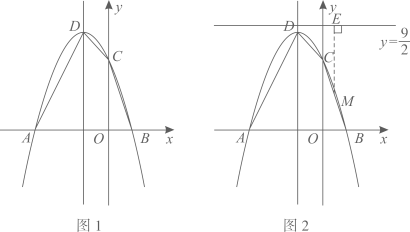
如图1,抛物线y=ax2+bx+3(a≠0)与x轴交于A(-3,0)和B(1,0),与y轴交于点C,顶点为D.
(1)
求解抛物线解析式;
(2)
连接AD,CD,BC,将△OBC沿着x轴以每秒1个单位长度的速度向左平移,得到  ,点O、B、C的对应点分别为点
,点O、B、C的对应点分别为点  ,
,  ,
,  ,设平移时间为t秒,当点O'与点A重合时停止移动.记
,设平移时间为t秒,当点O'与点A重合时停止移动.记  与四边形AOCD的重叠部分的面积为S,请直接写出S与时间t的函数解析式;
(3)
如图2,过抛物线上任意一点M(m,n)向直线l:
与四边形AOCD的重叠部分的面积为S,请直接写出S与时间t的函数解析式;
(3)
如图2,过抛物线上任意一点M(m,n)向直线l:  作垂线,垂足为E,试问在该抛物线的对称轴上是否存在一点F,使得ME-MF=
作垂线,垂足为E,试问在该抛物线的对称轴上是否存在一点F,使得ME-MF=  ?若存在,请求F点的坐标;若不存在,请说明理由.
?若存在,请求F点的坐标;若不存在,请说明理由.
【考点】
待定系数法求二次函数解析式;
勾股定理;
二次函数y=ax²+bx+c的图象;
二次函数y=ax²+bx+c的性质;
能力提升

