1.
定义:若四边形有一组对角互补,一组邻边相等,且相等邻边的夹角为直角,像这样的图形称为“直角等邻对补”四边形,简称“直等补”四边形,根据以上定义,解决下列问题:
(1)
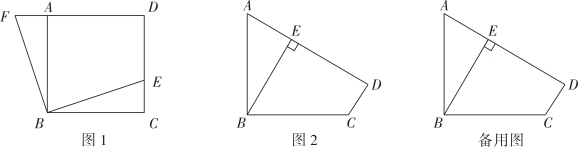
如图1,正方形  中,E是
中,E是  上的点,将
上的点,将  绕B点旋转,使
绕B点旋转,使  与
与  重合,此时点E的对应点F在
重合,此时点E的对应点F在  的延长线上,则四边形
的延长线上,则四边形  为“直等补”四边形,为什么?
(2)
如图2,已知四边形
为“直等补”四边形,为什么?
(2)
如图2,已知四边形  是“直等补”四边形,
是“直等补”四边形,  ,
,  ,
,  ,点
,点  到直线
到直线  的距离为
的距离为  .
.
①求 的长.
②若M、N分别是 、
边上的动点,求
周长的最小值.
【考点】
勾股定理;
正方形的性质;
相似三角形的判定与性质;
旋转的性质;
定义新运算;
能力提升